Kostenvergleichsrechnung

#Definition

Bei der Kostenvergleichsrechnung werden zur Beurteilung von Investitionen lediglich deren (durchschnittlichen) Kosten einer Periode (Jahr) analysiert und verglichen, um die kostengünstigere Alternative zu ermitteln.
Die Erlöse bleiben unberücksichtigt.

#Kostenarten

Personalkosten
- Löhne und Gehälter
- Lohnnebenkosten
Sachkosten
- Materialkosten
- Instandhaltungskosten
- Raumkosten
- Energiekosten
Kalkulatorische Kosten
- kalkulatorische Abschreibungen
- kalkulatorische Zinsen

#Kalkulatorische Abschreibungen

In der Investitionsrechnung wird in der Regel linear abgeschrieben. Daher gilt:

$$ Afa (p. a.) =\frac {AW - RW}{n} $$

AW = Anschaffungswert
RW = Restwert
n = Nutzungsdauer

#Kalkulatorische Zinsen

Um eine gleichbleibende Verzinsung darzustellen wird auf die durchschnittliche Kapitalbindung zurückgegriffen:

$$ Zinsen = \frac {AW + RW}{2} *i $$

AW = Anschaffungswert
RW = Restwert
i = Zinssatz

#Exkurs: Wo finde ich den kalkulatorischen Zinssatz?

Der kalkulatorischen Zinssatz ist im Klausurkontext meistens vorgegeben, in der Realität findet man den Zinssatz in der Haushaltssatzung der jeweiligen Gemeinde.

#Übungsaufgabe 1 - Erwerb eines Druckers

#Sachverhalt

Es soll ein Drucker angeschafft werden und es gibt zwei Angebote zur Auswahl. Der kalkulatorische Zinssatz ist auf 7% festgelegt. Die zu erwartende Druckmenge beträgt jeweils 25.000 Seiten.

Alternative	A	B
Anschaffungskosten	2.600,-	3.150,-
Nutzungsdauer	4 Jahre	6 Jahre
Papierkosten pro Kopie	0,01	0,015
Tonerkosten pro Kopie	0,01	0,02
fixe Energiekosten pro Jahr	650	450
variable Energiekosten pro Kopie	0,02	0,01
Reparaturkosten pro Jahr	100,-	150,-

#Lösung Sachverhalt 1

Alternative	A	B
kalkulatorische Abschreibungen	650,-	525,-
kalkulatorische Zinsen	91,-	110,25
Papierkosten	250,-	375,-
Tonerkosten	250,-	500,-
fixe Energiekosten	650,-	450,-
variable Energiekosten	500,-	250,-
Reparaturkosten	100,-	150,-
Gesamt	2.491,-	2.360,25

Dem Drucker B ist also der Vorzug zu geben, da die Gesamtkosten am geringsten sind.

#Ermittlung der kritischen Menge

Bei der Kostenvergleichsrechnung ermittle ich bei einer festgelegten Menge (input) die vorteilhaftere Variante anhand der minimalen Kosten. Wenn der Input jedoch variabel ist, kann es vorkommen, dass ja nach eingesetzter Menge ein unterschiedliches Ergebnis bzw. eine andere Entscheidung herauskommt.. Dieser Punkt an dem das Ergebnis zur einen oder anderen Seite "kippt" nennt man kritische Menge.

Bei der Ermittlung dieser kritischen Menge gibt es zwei Verfahren:

grafische Ermittlung: Bei der grafischen Ermittlung stelle ich die beiden Kostenverläufe anhand einer Wertetabelle oder mit der Zweipunktmethode in einem Koordinatensystem dar und kann dann anhand des Schnittpunktes der zwei Geraden die kritische Menge ablesen.
rechnerische Ermittlung: Bei der rechnerischen Ermittlung bilde ich die zwei Kostenfunktionen, setze sie gleich und löse sie nach der Variablen (x = Menge) auf.

#Übungsaufgabe 2 - Kauf eines Motortesters

#Sachverhalt 1

Es soll ein Motortester erworben werden. Es stehen zwei Varianten zur Auswahl. Der kalkulatorische Zins beträgt einheitlich 6% und es werden 500 Einsätze durchgeführt.

Variante	A	B
Anschaffungskosten	12.000,-	24.000,-
Nutzungsdauer	6 Jahre	6 Jahre
Personalkosten je Stunde	30,-	30,-
Energiekosten je Einsatz	1,-	0,75
Dauer je Einsatz	20 Minuten	12 Minuten

#Lösung Sachverhalt 1

Variante	A	B
kalkulatorische Abschreibungen	2.000,-	4.000,-
kalkulatorische Zinsen	360,-	720,-
Personalkosten	5.000,- (10,- * 500)	3.000,- (6,- * 500)
Energiekosten	500,- (1,- * 500)	375,- (0,75 * 500)
Gesamt	7.860,-	8.095,-

#Sachverhalt 2

Es werden dieselben Daten wie oben angenommen, lediglich die Menge der Einsätze ist variabel.

Aufgabe a): grafische Darstellung der Kostenverläufe
Aufgabe b): rechnerische Ermittlung der Einsätze, bei denen die Kosten gleich sind.

#Lösung Sachverhalt 2a)

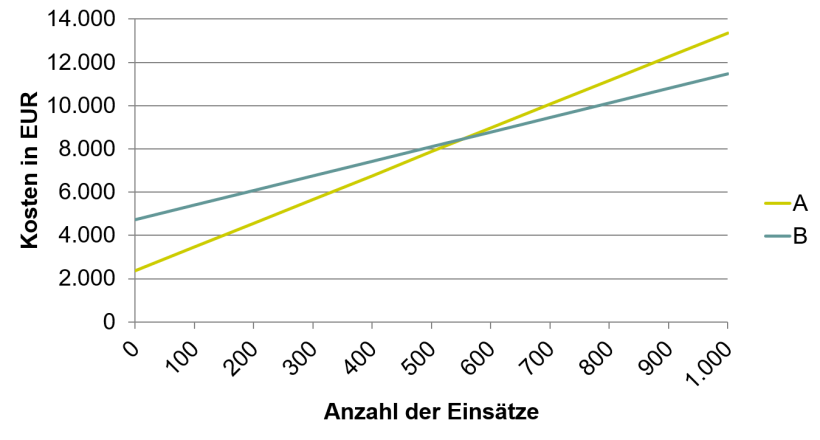
#Lösung Sachverhalt 2b)

Als erstes werden die beiden Kostenfunktionen aufgestellt:

$$ K(A) = 2.360 + 11x $$

$$ K(B) = 4.720 + 6,75x $$

Danach setzt man beide Kostenfunktionen gleich und löst die Gleichung nach "x" auf.

$$ 2.360 + 11x = 4.720 + 6,75x $$

$$ 4,25x = 2.360 $$

$$ x = 555,29 $$